
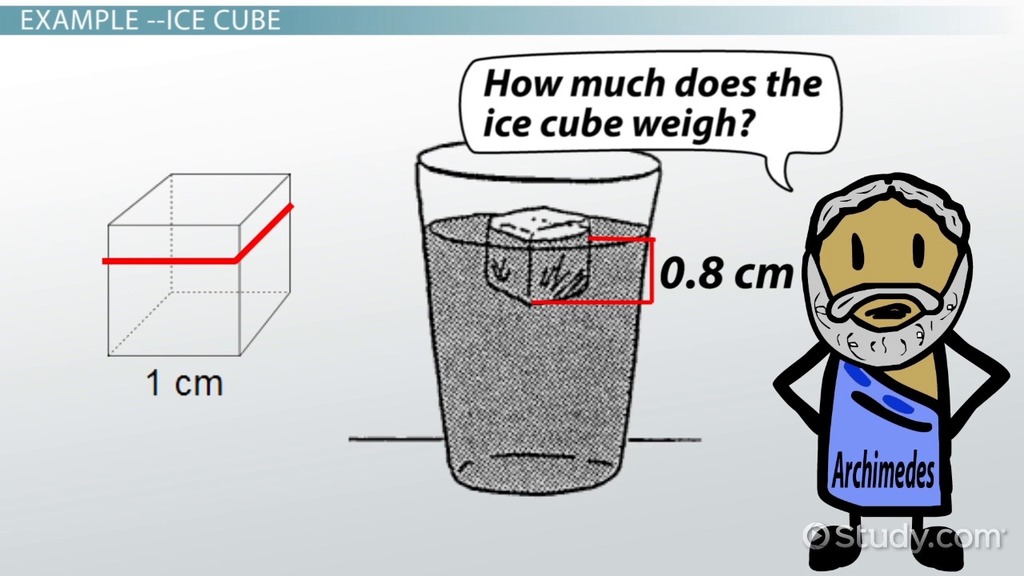
Since water has a density of 1 gram/cm3, this implies: It is clear that it has displaced m – m 2 = 80 g of water. It is then submerged in water and found to have apparent mass m 2 = 420 g P = Density m = Weight or Mass in Air m 2 = Weight in WaterĪn object is weighed in air and found to have mass m = 500 g It is known also as Hydrostatic Weighing. This method is quite commonly used in the construction industry. © OpenStax.Archimedes’ Principle aids in the determination of density by providing a convenient and accurate method for determining the volume of an irregularly shaped object, like a rock. We recommend using aĪuthors: Paul Peter Urone, Roger Hinrichs
Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the Similar behavior can be observed in contemporary physicists from time to time!
ARCHIMEDES PRINCIPLE HOW TO
He came up with his now-famous principle, saw how to apply it to determine density, and ran naked down the streets of Syracuse crying “Eureka!” (Greek for “I have found it”). Archimedes purportedly agonized over his task and had his inspiration one day while at the public baths, pondering the support the water gave his body. Even ancient peoples, however, realized that the density of gold was greater than that of any other then-known substance.
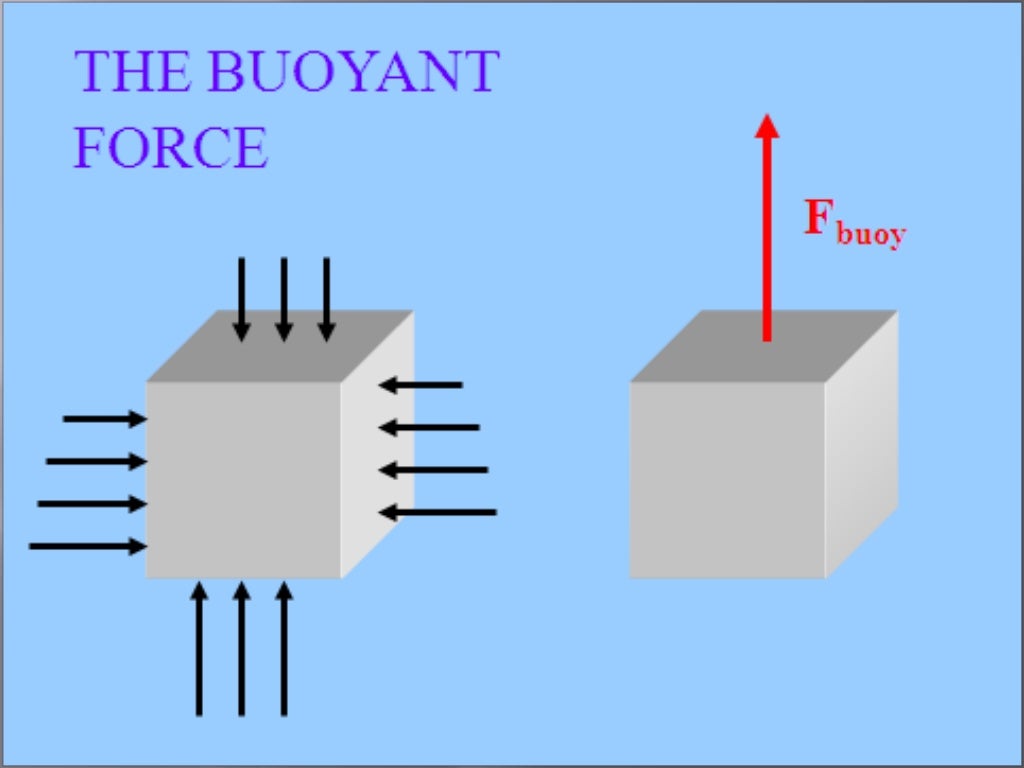
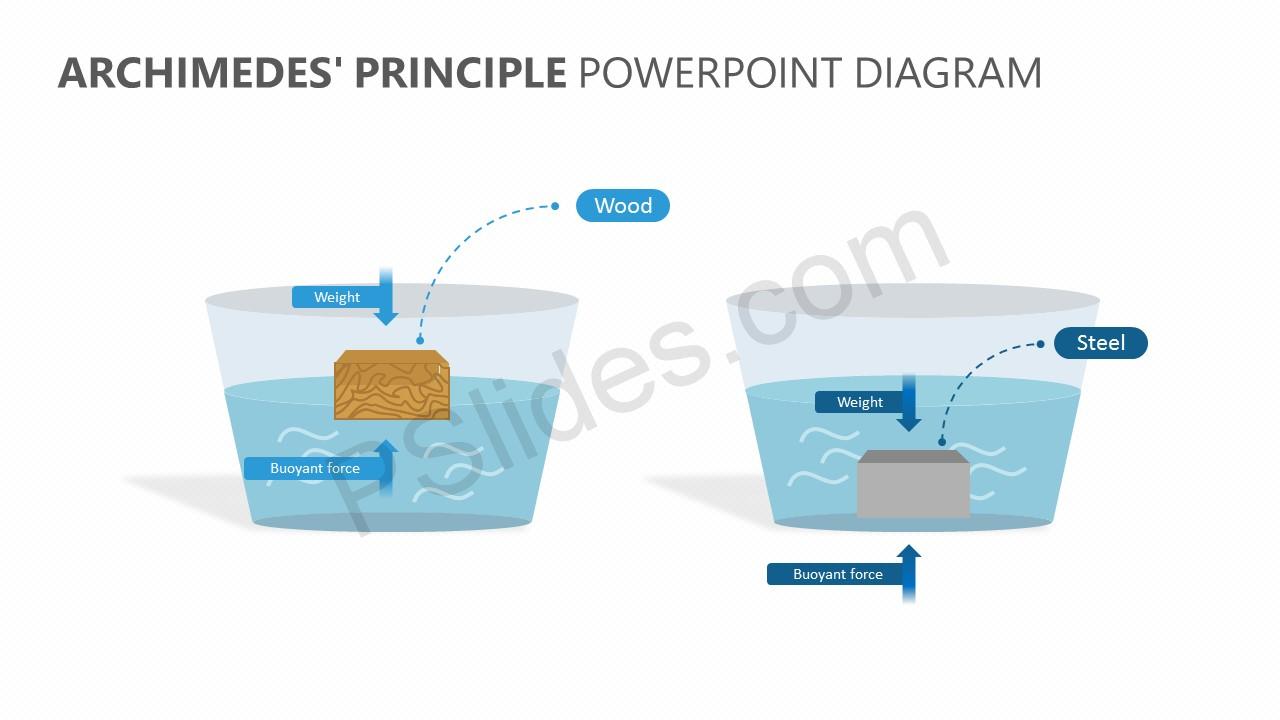
The purity of gold is difficult to determine by color (it can be diluted with other metals and still look as yellow as pure gold), and other analytical techniques had not yet been conceived. As the story goes, the king of Syracuse gave Archimedes the task of determining whether the royal crown maker was supplying a crown of pure gold. This brings us back to Archimedes’ principle and how it came into being. Most modern counterfeits are not pure silver. You can see from Table 11.1 that this density is very close to that of pure silver, appropriate for this type of ancient coin. We can now find the density of the coin using the definition of density: This is also the volume of the coin, since it is completely submerged. The buoyant force is always present whether the object floats, sinks, or is suspended in a fluid.įigure 11.20 (a) An object submerged in a fluid experiences a buoyant force F B F B size 12. If the buoyant force equals the object’s weight, the object will remain suspended at that depth. If the buoyant force is less than the object’s weight, the object will sink. (See Figure 11.19.) If the buoyant force is greater than the object’s weight, the object will rise to the surface and float. There is a net upward, or buoyant force on any object in any fluid. This means that the upward force on the bottom of an object in a fluid is greater than the downward force on the top of the object. (credit: Crystl)Īnswers to all these questions, and many others, are based on the fact that pressure increases with depth in a fluid. (credit: Allied Navy) (c) Helium-filled balloons tug upward on their strings, demonstrating air’s buoyant effect.

(b) Submarines have adjustable density (ballast tanks) so that they may float or sink as desired. Figure 11.18 (a) Even objects that sink, like this anchor, are partly supported by water when submerged.


 0 kommentar(er)
0 kommentar(er)
